Temporal Recalibration
By Sarah Booth (sarah.booth@le.ac.uk)
Background
Trends in survival over calendar time
Clinical risk prediction models should produce well-calibrated (accurate) predictions for patients who have been recently diagnosed with a particular health condition. However, often there are improvements in survival over time due to new treatments and healthcare policies. For example, survival following a diagnosis of cancer has improved over the past 20 years in many countries.
As we do not have long-term follow-up data for recently diagnosed patients, we have to rely on including patients who were diagnosed many years ago in order to develop prognostic models that can produce long-term survival predictions. However, if survival has improved over time, including these patients means that the predictions will be out-of-date and will under-estimate the survival of new patients.
This idea is illustrated in the graph below that shows the Kaplan-Meier curves increasing over calendar time. The Kaplan-Meier for the entire cohort (pink dashed line) is effectively an average of these curves and therefore does not provide an accurate estimate of the survival of the recently diagnosed patients.
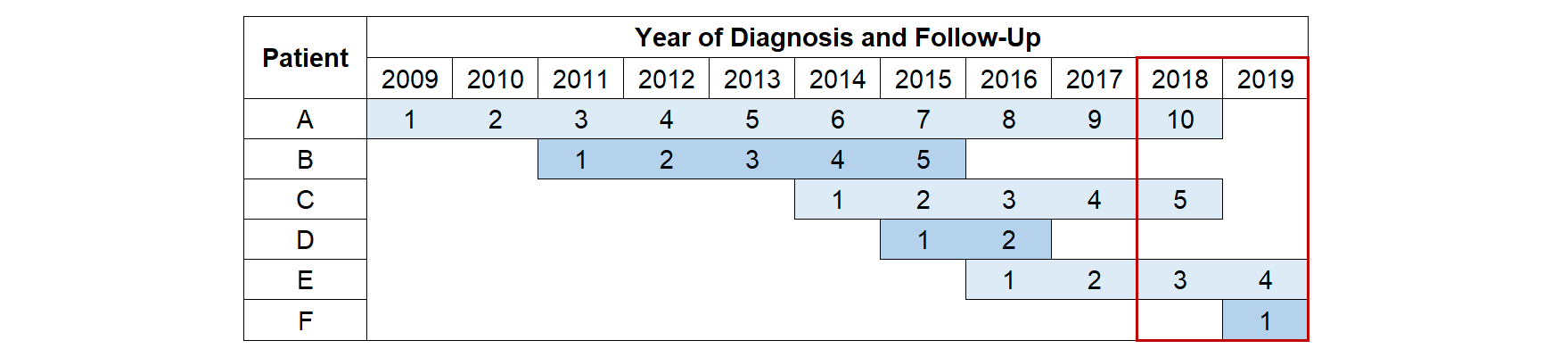
Period analysis
One approach for producing more up-to-date estimates of survival is to use period analysis. This ensures that only the most recent data is used to estimate the hazard rates using delayed entry. The period window (red box) defines the follow-up time and events that are included. Whilst people diagnosed 10 years ago can still contribute towards the analysis (Patient A), they only contribute towards the estimates of the long-term hazard rates. This allows the short-term hazards to be estimated from only the most recently diagnosed patients (Patient F) meaning that these estimates are as up-to-date as possible. Using this approach produces a Kaplan-Meier curve that agrees much more closely with the survival estimates of the recently diagnosed patients (grey dashed line).
The sample size and number of events are reduced as those who die before the period window are excluded (Patients B and D). Therefore, a disadvantage of using this method as the basis for developing a prognostic model is that this may limit the number of predictors that can be included in the model else it may lead to issues of overfitting.
Temporal Recalibration
Temporal recalibration aims to combine the advantage of having up-to-date estimates from period analysis with retaining the full dataset to estimate the predictor effects. It is a two-step process where the standard model is first developed as usual to obtain the predictor effects (linear predictor). The second step is to recalibrate the model by re-estimating the baseline in the subset defined by the period window whilst constraining the predictor effects to remain the same. This can be achieved by including the linear predictor as an offset term (if a PH model is fitted) or by adding constraints for the coefficients of each of the predictor parameters. The second approach will work even in the case of non-proportional hazards (note: if time-dependent effects are included in flexible parametric survival models, the same knot locations from the original model should also be used). Once this recalibration is performed, the predictions can be obtained as usual.
Example
In this example, I’ll show how to perform temporal recalibration when developing a prognostic model. I’ll also illustrate how this method can be beneficial when survival is improving over time by testing how well this model performs in producing predictions for recently diagnosed patients in comparison to using the standard method.
Data
The simulated data in this example is loosely based on survival following a diagnosis of cancer. The lower short-term and higher long-term hazards for more recent patients could occur if a new treatment delays deaths from occurring in the short-term. This leads to an overall improvement in survival over time as shown by the Kaplan-Meier curves.
This simulated dataset contains the following variables: ID number (id), year of diagnosis (yydx, 2009-2019), date of diagnosis (dx), date of death/censoring (exit), survival status (status, 0 = Alive, 1 = Dead), age at diagnosis (age, 44-93), sex (sex, 0 = Male, 1 = Female) and stage of tumour at diagnosis (stage, 1-3).
The derivation dataset (val=0) includes patients diagnosed between 2009 and 2019. In order to test how well temporal recalibration performs for making predictions for recently diagnosed patients, the validation dataset (val=1) includes patients diagnosed in 2019.
Model development
I’ll fit a simple prognostic model that contains age, sex and stage of tumour as predictors so I’ll first need to create the dummy variables relating to sex and stage.
In this example, I simulated the effect of age to be linear for simplicity so I’ll just model it as a linear term. However, in practice, age is often a non-linear effect and should instead be modelled using a method that can capture this trend such as restricted cubic splines or fractional polynomials. To make the baseline interpretable, I’ll centre the age variable on 70 (the mean age).
use https://www.pclambert.net/data/simulated_improvements, clear
tab stage, gen(stage)
gen female = sex == 1
gen age_centre = age-70
I’ll fit the following 3 models:
-
M1: The standard approach (not accounting for improvements in survival)
-
M2: Temporal recalibration of model M1 using a 5 year period window (2015-2019)
-
M3: Temporal recalibration of model M1 using a 2 year period window (2018-2019)
Here I’ll use stpm2 to fit flexible parametric survival models.
These models use restricted cubic splines to model the log cumulative
baseline hazard. This is my preferred approach for prognostic modelling since having a fully parametric baseline makes it easy to produce smooth predicted survival curves both in and out-of-sample. However, temporal recalibration can also be applied to Cox PH models using stcox which I’ll show later.
Standard method (no adjustments for survival improvements)
Firstly I’ll use stset to create the survival times of patients in the development dataset (val=0), censoring any individuals who are alive at the end of 2019 or after 10 years of follow-up.
. stset exit if val==0, origin(dx) fail(status==1) scale(365.25) ///
> exit(time min(dx+10*365.25,mdy(12,31,2019)))
Survival-time data settings
Failure event: status==1
Observed time interval: (origin, exit]
Exit on or before: time min(dx+10*365.25,mdy(12,31,2019))
Time for analysis: (time-origin)/365.25
Origin: time dx
Keep observations
if exp: val==0
--------------------------------------------------------------------------
64,913 total observations
9,863 ignored at outset because of if exp
--------------------------------------------------------------------------
55,050 observations remaining, representing
15,750 failures in single-record/single-failure data
227,227.58 total analysis time at risk and under observation
At risk from t = 0
Earliest observed entry t = 0
Last observed exit t = 10
The model can then be fitted. I’ll also store the model in memory and estimate the linear predictor for use when performing temporal recalibration. Using the xb option includes the parameters relating to the restricted cubic spline function in the baseline so the xbnobaseline option should be used to calculate the linear predictor.
. stpm2 age_centre female stage2 stage3, df(3) scale(hazard) noorthog
Iteration 0: log likelihood = -45144.513
Iteration 1: log likelihood = -45141.502
Iteration 2: log likelihood = -45141.5
Log likelihood = -45141.5 Number of obs = 55,050
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
xb |
age_centre | .0290524 .0013306 21.83 0.000 .0264445 .0316603
female | -.0793949 .0159424 -4.98 0.000 -.1106414 -.0481484
stage2 | 1.221257 .0273876 44.59 0.000 1.167578 1.274936
stage3 | 3.067474 .0264141 116.13 0.000 3.015703 3.119244
_rcs1 | .7857653 .0216787 36.25 0.000 .7432758 .8282548
_rcs2 | -.0027358 .0032212 -0.85 0.396 -.0090493 .0035777
_rcs3 | .0044443 .0047324 0.94 0.348 -.004831 .0137197
_cons | -3.730169 .0627114 -59.48 0.000 -3.853082 -3.607257
------------------------------------------------------------------------------
. estimates store standard
. predict lp, xbnobaseline
Temporal recalibration
To temporally recalibrate the model, stset is required to define the period analysis subsample. Firstly I’ll perform temporal recalibration using a 5 year window and then with a 2 year window to illustrate how the size of the window affects the sample size, number of events and the calibration of the resulting predictions.
To ensure that the predictor effects remain the same in the temporally recalibrated models, I’ll create a constraint to include the linear predictor as an offset term.
. stset exit if val==0, origin(dx) fail(status==1) scale(365.25) ///
> entry(time mdy(1,1,2015)) exit(time min(dx+10*365.25,mdy(12,31,2019)))
Survival-time data settings
Failure event: status==1
Observed time interval: (origin, exit]
Enter on or after: time mdy(1,1,2015)
Exit on or before: time min(dx+10*365.25,mdy(12,31,2019))
Time for analysis: (time-origin)/365.25
Origin: time dx
Keep observations
if exp: val==0
--------------------------------------------------------------------------
64,913 total observations
9,863 ignored at outset because of if exp
7,088 observations end on or before enter()
--------------------------------------------------------------------------
47,962 observations remaining, representing
8,662 failures in single-record/single-failure data
154,675.08 total analysis time at risk and under observation
At risk from t = 0
Earliest observed entry t = 0
Last observed exit t = 10
. constraint 1 _b[lp] = 1
. stpm2 lp, scale(hazard) noorthog constraints(1) df(3)
note: delayed entry models are being fitted
Iteration 0: log likelihood = -23120.497
Iteration 1: log likelihood = -23119.369
Iteration 2: log likelihood = -23119.369
Log likelihood = -23119.369 Number of obs = 47,962
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
xb |
lp | 1 (constrained)
_rcs1 | .8481359 .0387457 21.89 0.000 .7721958 .924076
_rcs2 | -.0256607 .0066633 -3.85 0.000 -.0387205 -.0126009
_rcs3 | .0452753 .010843 4.18 0.000 .0240233 .0665272
_cons | -4.130539 .0880844 -46.89 0.000 -4.303181 -3.957897
------------------------------------------------------------------------------
. estimates store recal5
Using a period window of 5 years reduced the sample size from 55,050 in the standard analysis to 47,962 and the number of events from 15,750 to 8,662. As you can see, using a narrower window of 2 years, reduced these further to 42,872 and 3,572 respectively.
. stset exit if val==0, origin(dx) fail(status==1) scale(365.25) ///
> entry(time mdy(1,1,2018)) exit(time min(dx+10*365.25,mdy(12,31,2019)))
Survival-time data settings
Failure event: status==1
Observed time interval: (origin, exit]
Enter on or after: time mdy(1,1,2018)
Exit on or before: time min(dx+10*365.25,mdy(12,31,2019))
Time for analysis: (time-origin)/365.25
Origin: time dx
Keep observations
if exp: val==0
--------------------------------------------------------------------------
64,913 total observations
9,863 ignored at outset because of if exp
12,178 observations end on or before enter()
--------------------------------------------------------------------------
42,872 observations remaining, representing
3,572 failures in single-record/single-failure data
70,571.919 total analysis time at risk and under observation
At risk from t = 0
Earliest observed entry t = 0
Last observed exit t = 10
. stpm2 lp, scale(hazard) noorthog constraints(1) df(3)
note: delayed entry models are being fitted
Iteration 0: log likelihood = -9242.6684
Iteration 1: log likelihood = -9237.6059
Iteration 2: log likelihood = -9237.5939
Iteration 3: log likelihood = -9237.5939
Log likelihood = -9237.5939 Number of obs = 42,872
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
xb |
lp | 1 (constrained)
_rcs1 | .8498527 .064545 13.17 0.000 .7233468 .9763587
_rcs2 | -.036646 .011776 -3.11 0.002 -.0597266 -.0135654
_rcs3 | .0669358 .020309 3.30 0.001 .0271308 .1067408
_cons | -4.34597 .1395017 -31.15 0.000 -4.619389 -4.072552
------------------------------------------------------------------------------
. estimates store recal2
Obtaining predictions
Once the models are fitted, the predictions for the external validation dataset can be produced as usual using the predict (or standsurv) command.
10-year survival
The 10-year survival predictions for each of the patients in the validation dataset can be calculated using the timevar() option.
gen t10 = 10
// Standard method
estimates restore standard
predict standard_10 if val==1, surv timevar(t10)
// Temporal recalibration
foreach model in "recal5" "recal2" {
estimates restore `model'
predict `model'_10 if val==1, surv timevar(t10)
}
Performing temporal recalibration updates the baseline survival of the model which increases the 10-year survival prediction for each of the individuals. Using a narrower period window further restricts the data used to estimate the short-term hazard rates which can result in more up-to-date survival estimates.
. summ standard_10 recal5_10 recal2_10
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
standard_10 | 9,863 .589459 .3104698 .0037656 .9353574
recal5_10 | 9,863 .5995616 .3100445 .0049988 .9385352
recal2_10 | 9,863 .6070969 .3094904 .0061271 .9408247
Predictions for individual patients
We can also produce survival curves for patients by specifying their covariate patterns. I’ll create predictions for the following individuals:
-
A man aged 70 at diagnosis with a stage 1 tumour (baseline of the model)
-
A woman aged 82 at diagnosis with a stage 2 tumour
-
A woman aged 53 at diagnosis with a stage 3 tumour
-
A man aged 85 at diagnosis with a stage 3 tumour
To make the predictions from the standard model, I can use the
at() and zeros options to specify the covariate pattern (remembering that
age was centred on age 70).
. range timevar10 0 10 101
(64,812 missing values generated)
. estimates restore standard
(results standard are active now)
. predict p1_standard, zeros surv timevar(timevar10)
. predict p2_standard, at(age_centre 12 female 1 stage2 1) ///
> zeros surv timevar(timevar10)
. predict p3_standard, at(age_centre -17 female 1 stage3 1) ///
> zeros surv timevar(timevar10)
. predict p4_standard, at(age_centre 15 stage3 1) ///
> zeros surv timevar(timevar10)
As the temporally recalibrated models were fitted by including the linear predictor as an offset term, I first need to calculate the value of the linear predictor for these covariate patterns before making the survival predictions from the model.
estimates restore standard
local p2 = _b[age_centre]*12 + _b[female] + _b[stage2]
local p3 = _b[age_centre]*(-17) + _b[female] + _b[stage3]
local p4 = _b[age_centre]*(15) + _b[stage3]
foreach model in "recal5" "recal2" {
estimates restore `model'
predict p1_`model', zeros surv timevar(timevar10)
predict p2_`model', at(lp `p2') zeros surv timevar(timevar10)
predict p3_`model', at(lp `p3') zeros surv timevar(timevar10)
predict p4_`model', at(lp `p4') zeros surv timevar(timevar10)
}
Here it can be seen that accounting for improvements in survival as part of model development led to higher survival predictions, where particular improvements can be seen in the survival predictions for the high risk patients. Using a narrower period window of 2 years led to the highest survival estimates. However, this choice is a bias-variance trade-off since the sample size and number of events used to estimate the baseline hazard is further reduced.
Marginal survival predictions
One approach to assess the calibration-in-the-large is to compare the marginal predicted survival to the marginal observed survival. The marginal survival is calculated by estimating the survival curves for each of the individuals in the validation dataset and then taking the average. This can be calculated using meansurv with the predict command or alternatively using standsurv.
$$ \bar{S}(t) = \frac{1}{N} \sum_{i=1}^{N} {\widehat{S}(t|x_i)} $$
The marginal observed survival can be quantified by calculating the Kaplan-Meier in the validation dataset. If the model is well-calibrated, these two measures should agree closely. The validation dataset contains patients who were diagnosed in 2019 and as this is simulated data we can estimate their 10-year observed survival by using follow-up data until 2030.
// Standard method
estimates restore standard
predict marg_standard if val==1, timevar(timevar10) meansurv
// Temporal recalibration
foreach model in "recal5" "recal2" {
estimates restore `model'
predict marg_`model' if val==1, timevar(timevar10) meansurv
}
// Observed survival
stset exit if val==1, origin(dx) fail(status==1) scale(365.25) ///
exit(time dx+10*365.25)
sts gen marg_obs = s
Here it can be seen that not accounting for trends in survival over time led to under-estimating the marginal survival across the full 10-year period. However, using temporal recalibration for model development improved the calibration of the survival predictions. Decreasing the size of the period window has the potential to produce more up-to-date estimates and here it can be seen that using a 2 year window produced the best agreement with the observed survival.
Cox PH models
In the above example, I’ve shown how to perform temporal recalibration using flexible parametric survival models. However, temporal recalibration can also be applied when fitting PH Cox models. The only difference is that offset() is used instead of constraints().
stset exit if val==0, origin(dx) fail(status==1) scale(365.25) ///
exit(time min(dx+10*365.25,mdy(12,31,2019)))
stcox age_centre female stage2 stage3
predict lp_cox, xb
stset exit if val==0, origin(dx) fail(status==1) scale(365.25) ///
entry(time mdy(1,1,2015)) exit(time min(dx+10*365.25,mdy(12,31,2019)))
stcox, estimate offset(lp_cox)
References
Arnold, M. et al. Progress in cancer survival, mortality, and incidence in seven high-income countries 1995-2014 (ICBP SURVMARK-2): a population-based study. The Lancet Oncology 2019; 20(11): 1493-1505
Brenner, H. & Gefeller, O. An alternative approach to monitoring cancer patient survival. Cancer 1996; 78(9): 2004-2010
Booth, S.; Riley, R. D.; Ensor, J.; Lambert P. C. & Rutherford, M. J. Temporal recalibration for improving prognostic model development and risk predictions in settings where survival is improving over time. International Journal of Epidemiology 2020; 49(4): 1316–1325